[RecSys] 5. 협업 필터링 기반 추천시스템 만들기 - 이론편1 (feat.유사도)

본 포스팅에서는 본격적으로 선형 회귀를 활용하여 협업필터링 추천시스템을 만들어보겠다.

협업필터링 추천 시스템의 개념은 아래 포스팅 참고 

https://ysryuu.tistory.com/24

[RecSys] 4. 협업 필터링이란?

 

1. 데이터 표현

협업 필터링을 위해서는 데이터를 어떻게 수학적으로 표현해야 할까?

내용기반 필터링에서는 각 유저에 대해서 액션, 로맨스, 감동 등의 영화 속성을 활용해 영화에 대한 선호도를 표시했었다.

협업 필터링에서는 영화의 내용, 즉 속성은 문제가 되지 않고, 각 유저와 영화의 관계가 문제가 되기 때문에 

아래와 같이 유저들의 리스트와, 유저들의 영화에 대한 평점 데이터가 있으면 된다. 

 

 

 

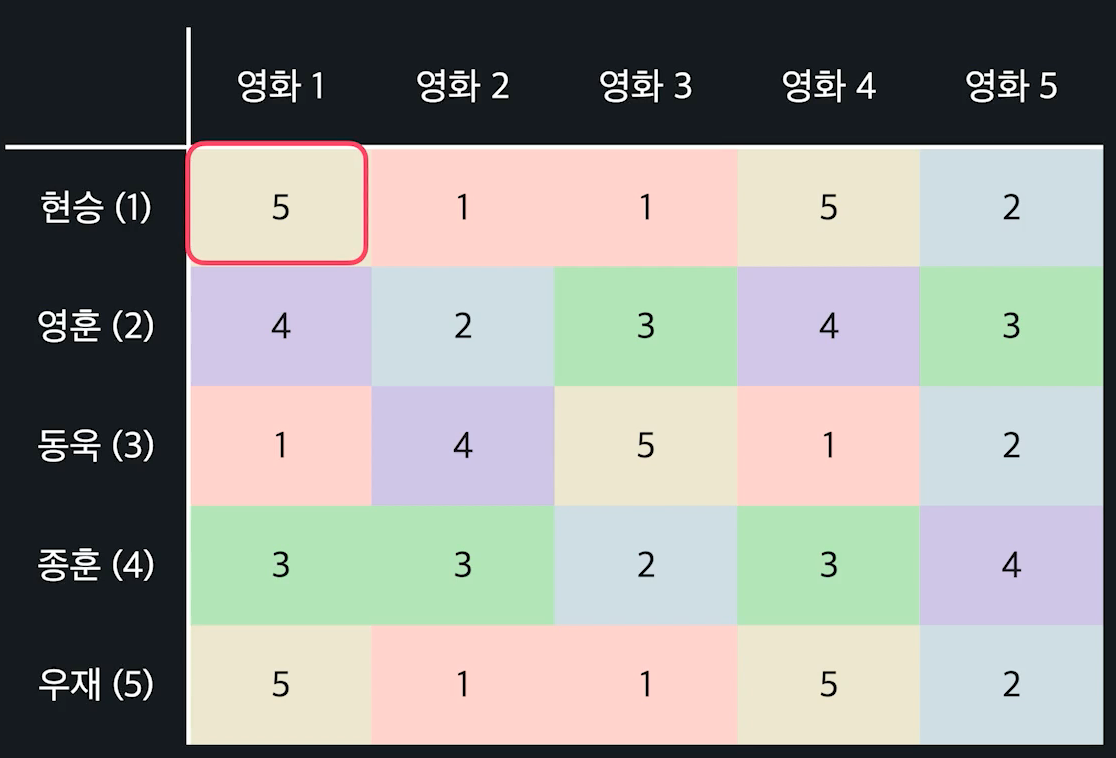
현승의 영화에 대한 평점은 아래와 같이 나타낼 수 있다 

$$ r^{(1)} = \begin{bmatrix} 5 \\ 1 \\ 1 \\ 5 \\ 2 \end{bmatrix} $$

이를 일반화 한다면, 유저 a의 영화 i에 대한 평점은 아래와 같이 표현 가능하다 

$$ r_{i}^{(a)} $$

 

---

2. 비슷한 유저 정의 

그렇다면, 협업 필터링을 위해 '비슷한 유저'를 정의하는 기준은 어떻게 결정해야 할까?

이 문제는 데이터간 '거리' 개념을 알아야 한다. 만약 두 유저간의 거리가 가깝다면, 둘은 유사 / 비슷한 그룹의 유저라고 볼 수 있을 것이다.

 

유사도를 계산하는 대표적인 방식에는 두가지가 있다 : 유클리드 거리와 코사인 유사도이다.

아래 그림에서 A와 B 간의 유사도를 측정할 때,

유클리드 거리는 dist(A,B)로 A와 B 사이의 거리를 측정하는 반면, 

코사인 유사도는 Cos θ 로, A와 B 사이에 벌어진 각도를 측정하는 개념이다.

https://www.researchgate.net/figure/The-difference-between-Euclidean-distance-and-cosine-similarity_fig2_320914786

 

 

1) 유클리드 거리 (Eucledian distance) : 거리기반 유사도 

 

먼저 유클리드 거리 개념을 알아보자.

유클리드 거리의 수학적 정의는 '두 벡터 간의 직선 거리', 사분면 위에서 두 점 사이의 거리를 계산하는 식과 동일하다.

$$ d(v,w) = \sqrt{\sum_{i=1}^{n}(v_{i} - w_{i})^2} $$

 

유클리드 거리를 정의하는 함수를 코드로 표현하면, 아래와 같다.

import numpy as np

def euclidean_distance(v1, v2): 
	return np.sqrt(np.sum((v1-v2)**2))

 

위의 영화 평점 사례라면, 유클리드 거리로 a,b 두 유저간의 거리를 나타내는 식은 다음과 같을 것이다. 

모든 영화의 개수가 n일때, 영화들의 평점에 대해서 a, b 두 유저간 평점 차이 사이의 거리를 구하는 개념이다.

 

$$ dist(a,b) = \sqrt{(r_{1}^{(a)} - r_{1}^{(b)})^2 + (r_{2}^{(a)} - r_{2}^{(b)})^2 + ... + (r_{n}^{(a)} - r_{n}^{(b)})^2 } $$

 

이를 더욱 일반화해 표현하면 아래와 같다.

$$ dist(a,b) = \sqrt{\sum_{i=1}^{n}(r_{i}^{(a)} - r_{i}^{(b)})^2} $$

 

 

2) 코사인 유사도 (Cosine similarity) : 각도기반 유사도

 

다음으로 코사인 유사도를 알아보자. 

코사인이란, 직각 삼각형에서, 빗변과 두 변의 비율을 나타내는 삼각 함수이다. 

코사인은 각도가 주어졌을때, 직각 삼각형의 '빗변 길이 / 인접 변의 길이' 와 같다. 코사인 함수는 주어진 각도에 대한 빗변과 인접변의 비율을 계산한다.

 

 

코사인 함수 값은 위 그래프를 따르며, 코사인 함수의 값은 -1에서 1까지의 범위를 가지는데, 각도가 0°일 때 코사인 값은 1이며, 90°일 때는 0이고, 180°일 때는 -1이라는 값을 가지게 된다.

 

코사인 유사도의 수학적 정의는 '두 벡터 간의 각도', 사분면 위에서 두 점 사이의 각도, 즉 방향적 유사성을 계산한다.

 

$$ d(v,w) = 1- \frac{v\cdot w}{\left\|v\right\|\cdot \left\|w\right\|} $$ $$ cos(\theta)= \frac{A\cdot B }{\left\| A\right\| \times \left\| B\right\|}= \frac{\sum_{i=1}^{n}A_{i}B_{i}}{\sqrt{\sum_{i=1}^{n}A_{i}^{2}} \sqrt{\sum_{i=1}^{n}B_{i}^{2}}} $$

 

코사인 유사도를 정의하는 함수를 코드로 표현하면, 아래와 같다.

def cosine_similarity(v1,v2): 
    dot_product = np.dot(v1, v2) 
    norm_v1 = np.linalg.norm(v1)
    norm_v2 = np.linalg.norm(v2)
    return dot_product / (norm_v1 * norm_v2)

 

 

 

 

유클리드 거리 vs 코사인 유사도 

 

유클리드 거리와 코사인 유사도 간 가장 직관적인 차이는 코사인 유사도에서는 각 벡터의 값, 즉 선의 크기가 중요하지 않다는 점이다.

 

또한 유저 A와 가장 비슷한 유저들을 찾을 때 유클리드 거리로는 '거리가 가장 작은' 유저를 찾아야 하는 반면,

코사인 유사도로는 '유사도가 가장 큰' 유저를 찾아야 한다.

 

 

---

* 참고자료 

https://www.researchgate.net/figure/The-difference-between-Euclidean-distance-and-cosine-similarity_fig2_320914786