Question1 - [미들러] 카펫
문제설명 https://school.programmers.co.kr/learn/courses/30/lessons/42842
Leo는 카펫을 사러 갔다가 아래 그림과 같이 중앙에는 노란색으로 칠해져 있고 테두리 1줄은 갈색으로 칠해져 있는 격자 모양 카펫을 봤습니다.

Leo는 집으로 돌아와서 아까 본 카펫의 노란색과 갈색으로 색칠된 격자의 개수는 기억했지만, 전체 카펫의 크기는 기억하지 못했습니다.
Leo가 본 카펫에서 갈색 격자의 수 brown, 노란색 격자의 수 yellow가 매개변수로 주어질 때 카펫의 가로, 세로 크기를 순서대로 배열에 담아 return 하도록 solution 함수를 작성해주세요.
제한사항
- 갈색 격자의 수 brown은 8 이상 5,000 이하인 자연수입니다.
- 노란색 격자의 수 yellow는 1 이상 2,000,000 이하인 자연수입니다.
- 카펫의 가로 길이는 세로 길이와 같거나, 세로 길이보다 깁니다.
문제풀이
trial1
상대적으로 문제도 짧고 단순해보이나 조건을 어떻게 만족시키냐가 중요해 보였던 문제.
우선 brown과 yellow 개수의 합이 전체 카펫의 블록 개수인 total 이고,
카펫의 전체 크기를 구해야 하니 total 자연수를 두 쌍씩 소인수분해해서 조건을 만족하는 쌍을 출력하는 개념으로 풀었다.
여기서 중요한 조건은
1) 가로 길이가 세로 길이 이상이라는 점
2) yellow와 brown의 배열은, yellow가 brown에 둘러 쌓여 있어야 한다는 점.
이에 따라서 1부터 total의 반까지 돌면서,
1) 두 쌍 중 row가 col보다 크다는 조건과
2) 전체 row-2와 col-2를 곱하면 yellow 블록의 수라는 조건을 만족하는 값에 대해서만 출력하였다.
def solution(brown, yellow):
total = brown + yellow
lst = []
for i in range(1,total//2 +1) :
if total % i == 0 :
row = max(total/i, i)
col = min(total/i, i)
if (row-2) * (col-2) == yellow :
return [row,col]
*** 완전탐색 개념 (Brute Force)
문제를 풀고보니 카펫 문제도 완전 탐색 개념으로 푼 것이었다.
위 코드에서는 아래의 단계를 따라 완전 탐색하였다.
- 가능한 모든 길이 조합 탐색: 가능한 모든 길이 조합을 탐색하면서 각 조합이 전체 타일 수를 만족하는지 확인
- 조건 검사: 각 조합의 가로가 더 큰 경우 확인, 에 대해 테두리를 제외한 중앙 부분이 주어진 노란 타일 수와 일치하는지 확인
- 해 결정: 조건을 만족하는 첫 번째 조합을 찾아 해를 구하기
이처럼 완전탐색이란 가능한 모든 경우의 수를 하나씩 전부 다 검사하여 문제의 해를 찾는 방법이다.
Brute Force라는 말이 드러내듯이, 무식하게.. 무분별하게 (?) 가능한 모든 경우를 시도해 답을 찾는 방식이다.
구현이 쉽고 해를 항상 찾을 수 있어서 가장 단순하고 직관적인 방법이지만,
경우의 수가 많아지면 계산 시간이 급격히 증가하므로 비효율적이 될 수 있어서 주의 해야 한다.
완전탐색을 사용하는 조건은 아래와 같다.
- 문제의 크기가 작아서 모든 경우를 시도해도 시간이 크게 걸리지 않는 경우.
- 문제의 해가 반드시 존재하고, 모든 경우를 다 시도해야 확실한 해를 찾을 수 있는 경우.
- 최적화된 알고리즘을 생각해내기 전에 문제를 해결하는 첫 단계로 사용할 경우.
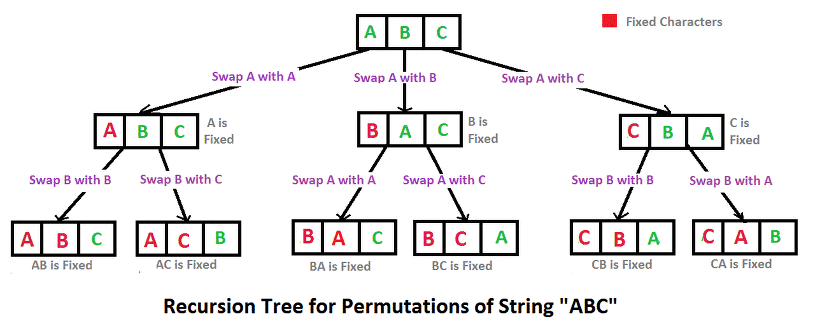
가장 대표적이고 전형적인 완전탐색의 예시는 순열 예시 (Permutation) 이다.
문자열의 모든 순열, 'ABC'를 찾는 경우 아래와 같이 모든 순열을 생성한 후 검사한다.
from itertools import permutations
def find_permutations(s):
# 모든 순열을 생성
perm = permutations(s)
# 각 순열을 출력
for p in perm:
print(''.join(p))
find_permutations("ABC")
# 출력 결과
ABC
ACB
BAC
BCA
CAB
CBA
배열 [1,2,3]의 모든 부분집합을 찾는 경우도 아래처럼 마찬가지이다.
def find_subsets(nums):
n = len(nums)
subsets = []
for i in range(2**n):
subset = []
for j in range(n):
if (i & (1 << j)) > 0:
subset.append(nums[j])
subsets.append(subset)
return subsets
result = find_subsets([1, 2, 3])
for subset in result:
print(subset)
# 출력 결과
[]
[1]
[2]
[1, 2]
[3]
[1, 3]
[2, 3]
[1, 2, 3]'Dev' 카테고리의 다른 글
| [코테] 99클럽 코테 스터디 12일차 TIL - BFS (feat.최단경로) (0) | 2024.06.01 |
|---|---|
| [코테] 99클럽 코테 스터디 10일차 TIL - 완전탐색 (0) | 2024.05.30 |
| [코테] 99클럽 코테 스터디 8일차 TIL - 정렬 (0) | 2024.05.27 |
| [코테] 99클럽 코테 스터디 5일차 TIL - 힙 (0) | 2024.05.24 |
| [코테] 99클럽 코테 스터디 4일차 TIL - 스택/큐 (0) | 2024.05.23 |