[알고리즘] 피보나치 수열

 

피보나치 수열이란? (Fibonacci Algorithm)

피보나치 수열이란, 

첫째, 둘째 항이 1이고 그 뒤의 항이 바로 앞의 두 항의 합인 수열을 말한다. 

인터넷에 피보나치 수열을 검색하면 다양한 이미지들을 보게되는데, 모두 동일한 수열을 뜻하는 것이 맞다.

 

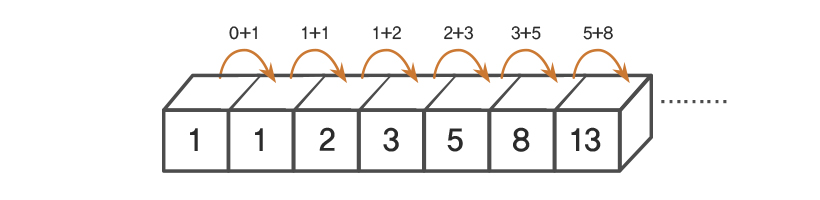
가장 기본적인 수열의 규칙을 드러내는 형태로는 아래 그림인데, 규칙과 수열을 알 수 있다.

아래 수열에서 이렇게 나오는 각 항의 수들을 '피보나치 수(Fibonacci number)' 이라고 하며, 아래 공식을 만족하는 수열 관계를 가진다.

$$ F_{n+2} = F_{n+1} + F_{n} $$

 

출처 : https://news.samsungdisplay.com/23402/

 

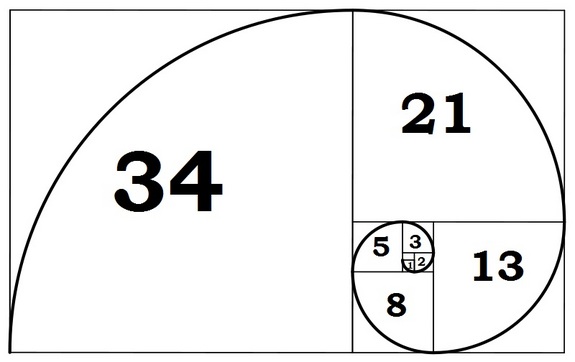
일렬로 배열된 수열 뿐 아니라, 피라미드 형식으로, 역삼각형 형태의 수의 관계가 위의 두개 값의 합이 아래의 값을 나타낸다고 볼 수도 있다.

출처 : https://velog.io/@southbig89/

또한 황금비에 수렴하는 성질도 있어서, 피보나치 수열의 인접한 두 항의 비율(Fn+1/ Fn)은 황금비(1: 1.16180339887) 에 수렴한다고 한다.

출처 : https://woodforest.tistory.com/166

 

피보나치 함수를 만드는 다양한 방법 

1. 일반 함수로 구하기 

>>> def fib(n) : 
...     a,b = 1,1   # 초기화
...     if n==1 or n==2 :  # 첫번째, 두번째 항 == 1
...             return 1
...     for i in range(1,n) :  # 반복마다 a에는 b, b에는 a+b를 할당하며 숫자 더해나감
...             a,b = b,a+b
...     return a   #n번째 수열 값

>>> fib(10)
55

# 수열 구하기 
>>> [fib(x) for x in range(1,11)]

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

 

2. 재귀함수로 구하기 

 

재귀함수로 자기 자신을 다시 호출하면서 피보나치 수열을 구하는 방식이다. 

>>> def fib(n) : 
...     if n==1 or n==2 : 
...             return 1
...     else : 
...             return fib(n-1) + fib(n-2)

>>> fib(10)
55

 

그림으로 치면 아래와 같은 방법으로, 이전의 피보나치 수열들의 값의 합을 구하는 것과 같다.

 

 

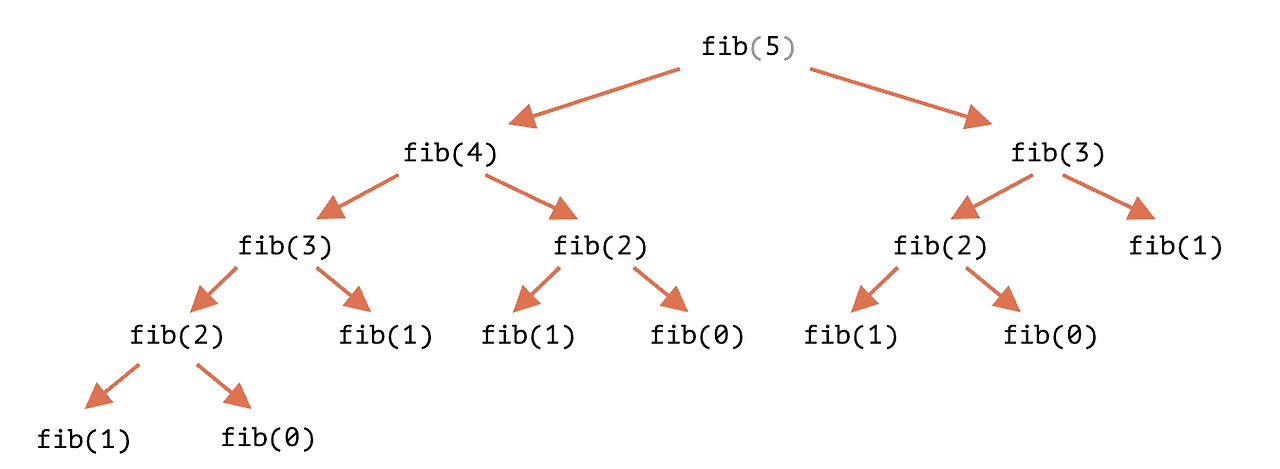
3. 제네레이터(Generator)로 구하기 

 

제네레이터를 활용해서 구할수도 있다. 아래 함수에서 fib(n) 자체가 제네레이터 객체로 생성된다. 

fib(n)을 프린트 해서 피보나치 수열을 확인할 수 있다.

>>> def fib(n) : 
...     a,b = 1,1
...     for i in range(n) : 
...             yield a 	# 값을 하나씩 반환한다 
...             a,b = b, a+b
...     return a		


>>> for x in fib(10) :  # 피보나치 수열 출력
...     print(x, end = ' ')

1 1 2 3 5 8 13 21 34 55

 

4. 메모이제이션(Memoization)으로 구하기 (동적계획법)

 

메모이제이션은 "계산된 값을 저장해 두고 이를 재활용하여 반복 계산을 피하는 방법"으로,

동적 계획법(Dynamic Programming)의 한 형태이다. 

빅데이터 대규모 데이터 처리에서 사용되는 맵리듀스(MapReduce)와 같은 기술에서도 사용되며, 시간 및 메모리 비용을 절약한다는 의의가 있다.

 

피보나치 수열에서도 메모이제이션을 사용해서 수열을 계산할 수 있다.

 

>>> def fib(n, memo={}) :  # 빈 메모리 딕셔너리를 지정
...     if n in memo :   # n번째 피보나치 수열값이 저장되어있다면 해당 값 반환
...             return memo[n] 
...     if n <=2 :   # 초기 항 설정 (1,1)
...             return 1
...     memo[n]= fib(n-1, memo) + fib(n-2,memo)  # 이외의 경우 모두 재귀적으로 fib 호출
...     return memo[n]


>>> fib(10)
55

 

5. 람다 이용 

파이썬 lambda 함수를 이용해서 짧은 한줄 코딩으로도 피보나치 수열을 표현할 수 있다. 

>>> fib = lambda n : 1 if n<=2 else fib(n-1) + fib(n-2)
>>> fib(10)
55

>>> fib = lambda n, a=0, b=1 : a if n<= 0 else fib(n-1, b, a+b)
>>> fib(10)
55

 

6. 행렬 연산 이용 

마지막으로 행렬 연산을 이용해서 수열 표현이 가능하다. 

우선 피보나치 수열을 행렬로 나타내면 아래와 같다. 

$$ \left[ F(n) \atop F(n-1) \right] = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \left[ F(1) \atop F(0) \right] $$

 

 

>>> def multiply(a, b, x, y): # 두개의 벡터 곱하기 (a,b는 변환행렬의 각 원소 / x,y는 초기벡터) 
...     return x*(a+b) + a*y, a*x + b*y
... 
>>> def square(a, b): # 행렬을 제곱하기, 새로운 변환 행렬을 반환 
...     a2 = a * a
...     b2 = b * b
...     ab = a * b
...     return a2 + (ab << 1), a2 + b2 
... 
>>> def power(a, b, m): # 변환 행렬을 거듭제곱 하기 (m은 거듭제곱 지수) 
...     if m == 0:
...         return (0, 1)
...     elif m == 1:
...         return (a, b)
...     else:
...         x, y = a, b
...         n = 2
...         while n <= m:
...             # repeated square until n = 2^q > m
...             x, y = square(x, y)
...             n = n*2
...         # add on the remainder
...         a, b = power(a, b, m-n//2)
...         return multiply(x, y, a, b)
... 
>>> def implicit_fib(n):   # 변환행렬을 이용, 피보나치 수열의 n번째 값 계산) 
...     a, b = power(1, 0, n)
...     return a


>>> implicit_fib(10)
55

 

 

 

 

---

참고자료 - https://richwind.co.kr/3

피보나치(Fibonacci) 수열을 구현하는 7가지 방법 - 파이썬(Python) 피보나치 구현 7선

https://pacific-ruler.tistory.com/entry/Python-%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98-%EC%88%98%EC%97%B4-%EA%B5%AC%ED%98%84%ED%95%98%EA%B8%B0-%EC%97%AC%EB%9F%AC%EA%B0%80%EC%A7%80-%EB%B0%A9%EB%B2%95-%EC%97%85%EB%8D%B0%EC%9D%B4%ED%8A%B8-%EC%A4%91

파이썬 피보나치 알고리즘 구현 방법 (6가지)